AGC021B 题解
Zesty_Fox
2022-01-11 00:03:55
也许更好的阅读体验:[cnblogs](https://www.cnblogs.com/acceptedzhs/p/agc021b-sol.html)
不难发现其实就是在平面上随机取点。
首先要判断一个点被取到的概率是否为 $0$。设这个点为 $A$,显然,所有除 $A$ 以外的点都要在 $A$ 点同侧。枚举其周围 $3$ 个点 $B,C,D$,如果 $A$ 点在 $\triangle BCD$ 内部,则 $A$ 被取到的概率为 $0$。如图:

(能取到 $A$ 点的区域,即红色区域,面积是有限的,在无限的平面上随机取点,落到红色区域的概率为 $0$)
然后考虑怎么算概率。不难发现,我们只需将 $A$ 点与周围点连边,取所有边的中垂线,计算中垂线形成的的最小夹角即可。答案即为 $\frac{\text{最小夹角}}{2\pi}$。如图:
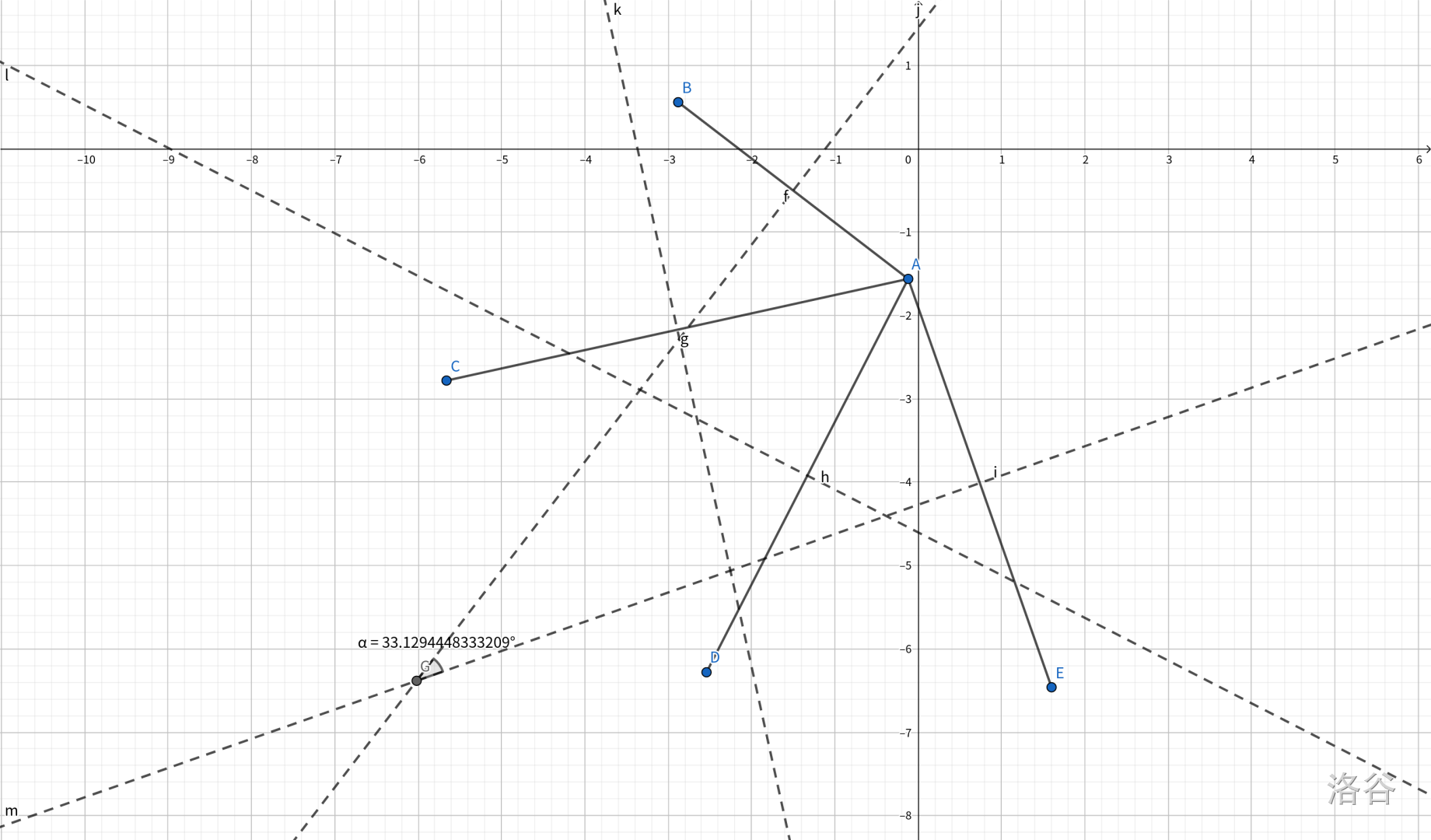
(最小夹角为 $\alpha$,即为 $\angle BAE$ 的补角)
只要极角排序或枚举两个点即可。
Code:
```cpp
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef vector<int> vi;
typedef pair<int,int> pii;
template<typename T>
inline T read(){
T x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*f;
}
#define rdi read<int>
#define rdll read<ll>
#define fi first
#define se second
#define pb push_back
#define mp make_pair
const int N=110;
const double pi=acos(-1);
int n;
pii p[N];
double deg[N][N],res[N];
int main(){
n=rdi();
for(int i=1;i<=n;i++) p[i].fi=rdi(),p[i].se=rdi();
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(i!=j) deg[i][j]=atan2(p[j].se-p[i].se,p[j].fi-p[i].fi);
for(int i=1;i<=n;i++){
bool flg=0;
for(int i1=1;i1<=n;i1++){
for(int i2=i1+1;i2<=n;i2++){
for(int i3=i2+1;i3<=n;i3++){
if(i1==i||i2==i||i3==i) continue;
double d[3]={deg[i][i1],deg[i][i2],deg[i][i3]};sort(d,d+3);
if(d[2]-d[0]>=pi&&d[2]-d[1]<pi&&d[1]-d[0]<pi) {flg=1;goto ed;}
}
}
}
ed:
if(flg) continue;
double ang=pi;
for(int i1=1;i1<=n;i1++){
for(int i2=i1+1;i2<=n;i2++){
if(i1==i||i2==i) continue;
double tmp=fabs(deg[i][i1]-deg[i][i2]);
if(tmp>=pi) tmp=2*pi-tmp;
ang=min(ang,pi-tmp);
}
}
res[i]=ang/(2*pi);
}
for(int i=1;i<=n;i++) printf("%.6lf\n",res[i]);
return 0;
}
```